Ein Thema, das mich insbesondere bei meinem Wikifolio sehr beschäftigt hat, ist die Frage der Wahl geeigneter Positionsgrößen. In diesem Zusammenhang habe ich viel über pauschale Regeln gelesen, wie z.B. „keine Position größer als x % des Portfolios“ – nur führt das aus meiner Sicht zu mittelmäßigen Ergebnissen – denn wenn ich von einer Position richtig überzeugt bin, warum sollte ich dann nicht stärker investiert sein?
Auf der Suche nach einem Konzept, wie ich das Chancen/Risiko-Profil der einzelnen Aktien bei der Wahl der Positionsgrößen berücksichtigen kann, bin ich im Buch von Edward O Thorp („Ein Mann für alle Märkte: Wie ich das Casino und den Markt geschlagen habe“) auf das sogenannte Kelly Kriterium gestoßen, das John Larry Kelly Junior entwickelt hat, um bei einem wiederholten Spiel (wie z.B. Roulette oder Poker) die Einsätze so zu wählen, dass das Risiko, sein gesamtes Geld zu verlieren, möglichst gering ist.
Die Kelly-Formel trifft die folgenden qualitativen Aussagen, die auch intuitiv gut nachvollziehbar sind:
- Je höher die erwartete Wertsteigerung des eingesetzten Kapitals, umso höher der Einsatz
- Je höher die Wahrscheinlichkeit des Gewinns, umso höher der Einsatz
- Nur bei 100% Erfolgswahrscheinlichkeit sollte das gesamte Kapital gesetzt werden
- Es gibt Situationen, in denen das Chancen-Risiko-Verhältnis so schlecht ist, dass man gar keinen Einsatz machen sollte
Die Formel, die diese Umstände beschreibt, sieht zunächst nicht ganz so intuitiv aus:

Mit
p: Erwartete Preissteigerung des Investments
w: Eintrittswahrscheinlichkeit für die Preissteigerung
Ein Beispiel zur Erläuterung: Eine Aktie notiert aktuell bei 100 EUR. Ihr erwartet eine Steigerung des Aktienkurses auf 200 EUR (p=+100%) mit einer Wahrscheinlichkeit von 60%.
Der maximale Depotanteil K ist demnach ((100% + 1) * 60 % -1) / 100% = ((1 + 1) * 0,6 -1)/ 1 = 0,2
D.h. der Wertanteil am Depot sollte 20% nicht überschreiten.
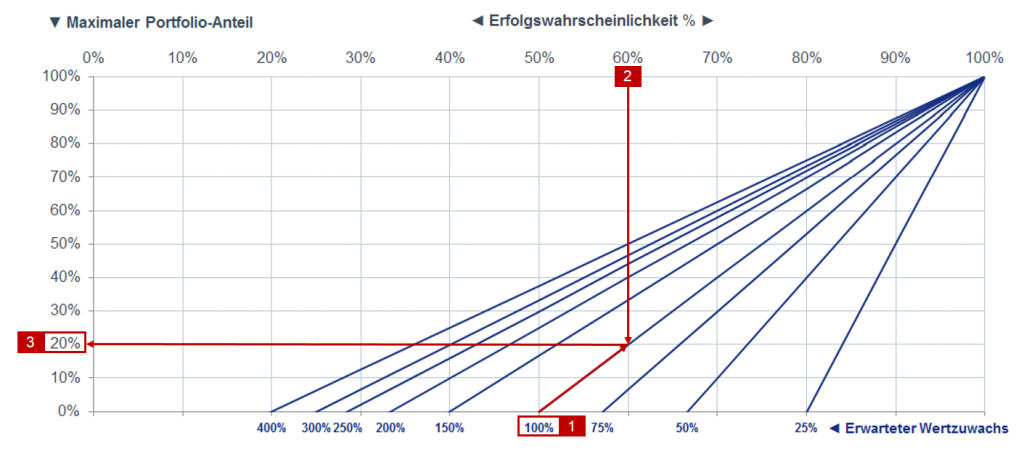
Wenn Euch das Rechnen zu kompliziert ist und ihr lieber direkt ablesen wollt, was das Kelly-Kriterium Euch erzählt, könnt ihr folgendes Diagramm nutzen – erläutert am obigen Beispiel:
Ihr geht von 100% erwartetem Wertzuwachs aus – also folgt ihr der blauen Linie, an der unten 100% steht (x-Achse) [1]. Dieser Linie folgt ihr bis zu dem Punkt, wo sie die senkrechte hellgraue Gitter-Linie mit der Erfolgswahrscheinlichkeit 60% schneidet [2]. Am Schnittpunkt beider Linien könnt ihr dann an der y Achse ablesen, dass der maximale Portfolio-Anteil 20% betragen sollte [3].
Praktische Anwendung
Das Kelly-Kriterium verwende ich auch bei der Wahl der Positionsgrößen in meinem Wikifolio „Minus Sinus Value Select„. In dem Wikifolio habe ich Clinuvel Pharmaceuticals ausgesprochen hoch gewichtet, und zwar im Schnitt mit ca. 50% – und dies ist laut Kelly-Kriterium auch die Größenordnung, die sich aus meiner Bewertung eines fairen Kursziels von 20-24 EUR ergibt. Nehmen wir also ein Kursziel von 22 EUR an und einen aktuellen Kurswert von 8 EUR, dann ist das Preissteigerungspotenzial p=22/8-1 = 175%. Da in dieser Bewertung auch Vitiligo mit einbezogen ist, nehme ich eine sehr konservative Erfolgswahrscheinlichkeit von 70% an.
Macht für den maximalen Depotanteil nach Kelly: K = ((1,75 +1)*0,7-1)/1,75=52,9%.
Grenzen Kelly-Kriteriums
Das Kelly-Kriterium wurde ursprünglich entwickelt, um eine endlose Serie von wiederholten Spielen (wie Roulette) zu simulieren – und das entspricht nicht der Herangehensweise in einem Aktiendepot, denn hier hat man in der Regel mehrere „Wetten“ gleichzeitig laufen. Bildlich gesprochen wäre das so, als ob man an mehreren Tischen gleichzeitig Roulette spielen würde. Da das Kelly-Kriterium aber nach einem Verlust auf ein geringeres Investitionsvolumen angewendet würde, liefert das Kelly-Kriterium vermutlich etwas zu hohe Werte für ein Aktiendepot (ohne dass ich das mathematisch beweisen könnte).
Darüber hinaus muss man sich einer Sache bewusst sein: Bei einem Roulette-Spiel, bei dem man keine Vorteile gegenüber der Bank hat (z.B. durch eine Prognosemethode für den Lauf der Kugel, wie Edward Thorp sie in seinem Buch beschreibt – er hat in den 1960er Jahren damit quasi den ersten Taschencomputer erfunden), würde das Kelly-Kriterium immer den Einsatz „0“ empfehlen – denn Roulette ist ein Spiel, bei dem über lange Zeiträume immer die Bank gewinnt, solange man nicht statistische Informationen zu seinem Vorteil („Edge“) nutzen kann. Analog ersetzt das Kelly-Kriterium nicht den „Edge“ des Investors bei der Auswahl seiner Aktien, sondern hilft ihm auf der Basis nur, die Höhe seines Wetteinsatzes zu kalibrieren.
Das Kursziel und damit die Preissteigerung zu ermitteln, dürfte für einen geschulten Value Investor weniger das Problem sein – schwieriger ist es jedoch für die Erfolgswahrscheinlichkeit. Denn faktisch kann es sein, dass der Markt niemals oder zumindest nicht zu Deinen Lebzeiten das Potenzial des Investments honoriert. Hierfür habe ich auch noch keine gute Lösung gefunden, habe mir aber selbst zur Regel gemacht, maximale Depotanteile nie über 50% gehen zu lassen – und diese Zahl sollte jeder hinsichtlich seiner persönlichen Risktoleranz anpassen. Die Erfolgswahrscheinlichkeit ist auch aus dem Grund schwierig, weil sie nur Gewinnen und Verlieren als Ergebnis kennt, wie eben beim Roulette, und bei einer Aktie gewinnt man immer noch, wenn nur 90% des Kursziels erreicht werden. Um dies abzubilden, empfiehlt es sich, verschiedene Szenarien zu rechnen – am Beispiel Clinuvel:
Szenario 1 (sehr pessimistisch): Die Aktie wird einen Kurs von 12 EUR erreichen, aber das mit einer hohen Wahrscheinlichkeit von 80%: K = 40%
Szenario 2 (pessimistisch): Die Aktie wird einen Kurs von 17 EUR erreichen, aber das mit einer hohen Wahrscheinlichkeit von 75%: K = 53%
Szenario 3 (neutral): Die Aktie wird einen Kurs von 22 EUR erreichen, aber das mit einer hohen Wahrscheinlichkeit von 70%: K = 53%
Szenario 4 (optimistisch): Die Aktie wird einen Kurs von 32 EUR erreichen, aber das mit einer hohen Wahrscheinlichkeit von 20%: K = -7%
Am Szenario 4 erkennt man schön die Grenzen des Kelly-Kriteriums – es gibt einen negativen Portfolio-Anteil an, d.h. man sollte gar nicht investieren. Und das ist auch die korrekte Antwort, wenn es nur ein Schwarz-Weiß Ergebnis gäbe (z.B. das Unternehmen ist insolvent: Ja/Nein). Gäbe es ein Roulette-Spiel wie Szenario 4, wäre das Ergebnis klar: Ich vervierfache meinen Einsatz (von 8 auf 32 EUR), aber habe nur eine 20% Gewinnchance (d.h. 1/5 vs Vervierfachung). Wenn man das oft genug spielt, hat man am Ende garantiert leere Taschen. Diese Tatsache ignoriert jedoch, dass es bei einer Aktie mehrere „Rückfallebenen“ (z.B. 90% Erreichung des Kursziels) gibt, die jeweils höhere Erfolgswahrscheinlichkeiten haben.
Als Fazit also: Eher defensive Annahmen für die Preissteigerung verwenden, und dadurch zu höheren Erfolgswahrscheinlichkeiten kommen. Wenn ihr feststellt, dass ihr zu sehr geringen Werten gelangt, dann stimmt vielleicht was mit Eurem Investment-Case nicht: Entweder ist das Risiko zu hoch für den zu erwarteten Gewinn, oder ihr seid Euch Eurer Sache nicht sicher (zu geringe Erfolgswahrscheinlichkeit). In einem solchen Fall lieber nicht an den beiden Zahlen p. In einem solchen Fall lieber nicht an den beiden Zahlen p & w rumschrauben, sondern zurück an den Schreibtisch und mehr Research betreiben!
… und nun viel Spaß bei der Anwendung des Kelly-Kriteriums – ich freue mich über Kommentare und Anregungen!
Keine Zeit, Dich jeden Tag um Dein Portfolio zu kümmern?
Wenn Du überzeugt vom Value Investing bist, aber Dich nicht täglich um Dein Depot kümmern möchtest oder nicht die Zeit für die notwendigen Analysen hast, dann gibt es einen einfachen Weg, von den Informationen auf dieser Seite zu profitieren – und zwar über mein Wikifolio „Minus Sinus Value Select“.
„Minus Sinus Value Select Wikifolio Musterdepot:
Wertsteigerung im Vergleich zu Indizes
Wikifolio: Minus Sinus Value Select
In diesem Musterdepot investiere ich gemäß der Grundsätze, die ich auf dieser Website erläutere. Die LANG & SCHWARZ Tradecenter AG & Co. KG hat ein besichertes Zertifikat herausgegeben, dass es Dir ermöglicht, an der Wertentwicklung des Musterdepots teilzuhaben.
Interesse? Hier geht’s zum Wikifolio Musterdepot „Minus Sinus Value Select“.


[…] Positionsgewichtung im Portfolio […]